NCEAce

MATHEMATICS – USEFUL FORMULAE

Official NZQA Level 3 Formulae Sheet • Provided during exams

Download Official PDF

ALGEBRA

Quadratics

ax2+bx+c=0  ⇒  x=−b±b2−4ac2aax^2+bx+c=0\;\Rightarrow\;x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}

Logarithms

y=log⁡bx  ⇔  x=byy=\log_b x\;\Leftrightarrow\;x=b^y
log⁡b(xy)=log⁡bx+log⁡by\log_b(xy)=\log_b x+\log_b y
log⁡b(xy)=log⁡bx−log⁡by\log_b\left(\frac{x}{y}\right)=\log_b x-\log_b y
log⁡b(xn)=nlog⁡bx\log_b\left(x^n\right)=n\log_b x
log⁡bx=log⁡axlog⁡ab\log_b x=\frac{\log_a x}{\log_a b}

Complex numbers

z=x+iyz=x+iy
z=r cis θz=r\,\mathrm{cis}\,\theta
z=r(cos⁡θ+isin⁡θ)z=r(\cos\theta+i\sin\theta)
z‾=x−iy\overline{z}=x-iy
z‾=r cis(−θ)\overline{z}=r\,\mathrm{cis}(-\theta)
z‾=r(cos⁡θ−isin⁡θ)\overline{z}=r(\cos\theta-i\sin\theta)
r=∣z∣=zz‾=x2+y2r=|z|=\sqrt{z\overline{z}}=\sqrt{x^2+y^2}
θ=arg⁡z\theta=\arg z
cos⁡θ=xr\cos\theta=\frac{x}{r}
sin⁡θ=yr\sin\theta=\frac{y}{r}

COORDINATE GEOMETRY

Straight Line

y−y1=m(x−x1)y-y_1=m(x-x_1)

CALCULUS

Differentiation

y = f(x)dy/dx = f'(x)
yy
f(x)  ⇒  dydx=f′(x)f(x)\;\Rightarrow\;\frac{dy}{dx}=f'(x)
ddx[ln⁡x]\frac{d}{dx}[\ln x]
1x\frac{1}{x}
ddx[eax]\frac{d}{dx}[e^{ax}]
aeaxae^{ax}
ddx[sin⁡x]\frac{d}{dx}[\sin x]
cos⁡x\cos x
ddx[cos⁡x]\frac{d}{dx}[\cos x]
−sin⁡x-\sin x
ddx[tan⁡x]\frac{d}{dx}[\tan x]
sec⁡2x\sec^2 x
ddx[sec⁡x]\frac{d}{dx}[\sec x]
sec⁡xtan⁡x\sec x\tan x
ddx[cosec⁡x]\frac{d}{dx}[\cosec x]
−cosec⁡xcot⁡x-\cosec x\cot x
ddx[cot⁡x]\frac{d}{dx}[\cot x]
−cosec⁡2x-\cosec^2 x

Integration

f(x)∫f(x)dx
∫xn dx\int x^n\,dx
xn+1n+1+c\frac{x^{n+1}}{n+1}+c
(n\neq -1)
∫1x dx\int \frac{1}{x}\,dx
ln⁡∣x∣+c\ln|x|+c
∫f′(x)f(x) dx\int \frac{f'(x)}{f(x)}\,dx
ln⁡∣f(x)∣+c\ln|f(x)|+c

Parametric Function

dydx=dydt⋅dtdx\frac{dy}{dx}=\frac{dy}{dt}\cdot\frac{dt}{dx}
d2ydx2=ddt(dydx)⋅dtdx\frac{d^2y}{dx^2}=\frac{d}{dt}\left(\frac{dy}{dx}\right)\cdot\frac{dt}{dx}

DIFFERENTIATION RULES

Product Rule

ddx[f(x)g(x)]=g(x)f′(x)+f(x)g′(x)\frac{d}{dx}[f(x)g(x)] = g(x)f'(x) + f(x)g'(x)
dydx=vdudx+udvdx\frac{dy}{dx} = v\frac{du}{dx} + u\frac{dv}{dx}
(If y = uv)

Quotient Rule

ddx[f(x)g(x)]=g(x)f′(x)−f(x)g′(x)g(x)2\frac{d}{dx}\left[\frac{f(x)}{g(x)}\right] = \frac{g(x)f'(x) - f(x)g'(x)}{g(x)^2}
dydx=vdudx−udvdxv2\frac{dy}{dx} = \frac{v\frac{du}{dx} - u\frac{dv}{dx}}{v^2}
(If y = \frac{u}{v})

Chain Rule

ddx[f(g(x))]=f′(g(x)) g′(x)\frac{d}{dx}[f(g(x))] = f'(g(x))\,g'(x)
dydx=dydududx\frac{dy}{dx} = \frac{dy}{du}\frac{du}{dx}
(If y = f(u) and u = g(x))

NUMERICAL METHODS

∫abf(x) dx≈12h[y0+yn+2(y1+y2+⋯+yn−1)]\int_a^b f(x)\,dx \approx \frac{1}{2}h\left[y_0 + y_n + 2\left(y_1 + y_2 + \cdots + y_{n-1}\right)\right]
(where h = \frac{b-a}{n} and y_r = f(x_r))
∫abf(x) dx≈13h[y0+yn+4(y1+y3+⋯ )+2(y2+y4+⋯ )]\int_a^b f(x)\,dx \approx \frac{1}{3}h\bigl[y_0 + y_n + 4(y_1 + y_3 + \cdots) + 2(y_2 + y_4 + \cdots)\bigr]
(where h = \frac{b-a}{n},\ y_r = f(x_r),\ n is even)

TRIGONOMETRY

cosec⁡θ=1sin⁡θ\cosec\theta=\frac{1}{\sin\theta}
sec⁡θ=1cos⁡θ\sec\theta=\frac{1}{\cos\theta}
cot⁡θ=1tan⁡θ\cot\theta=\frac{1}{\tan\theta}
cot⁡θ=cos⁡θsin⁡θ\cot\theta=\frac{\cos\theta}{\sin\theta}
asin⁡A=bsin⁡B=csin⁡C\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}
c2=a2+b2−2abcos⁡Cc^2=a^2+b^2-2ab\cos C
cos⁡2θ+sin⁡2θ=1\cos^2\theta+\sin^2\theta=1
tan⁡2θ+1=sec⁡2θ\tan^2\theta+1=\sec^2\theta
cot⁡2θ+1=cosec⁡2θ\cot^2\theta+1=\cosec^2\theta
If sin⁡θ=sin⁡α then θ=nπ+(−1)nα\text{If }\sin\theta=\sin\alpha\text{ then }\theta=n\pi+(-1)^n\alpha
(where n is any integer)
If cos⁡θ=cos⁡α then θ=2nπ±α\text{If }\cos\theta=\cos\alpha\text{ then }\theta=2n\pi\pm\alpha
(where n is any integer)
If tan⁡θ=tan⁡α then θ=nπ+α\text{If }\tan\theta=\tan\alpha\text{ then }\theta=n\pi+\alpha
(where n is any integer)
sin⁡(A±B)=sin⁡Acos⁡B±cos⁡Asin⁡B\sin(A\pm B)=\sin A\cos B\pm\cos A\sin B
cos⁡(A±B)=cos⁡Acos⁡B∓sin⁡Asin⁡B\cos(A\pm B)=\cos A\cos B\mp\sin A\sin B
tan⁡(A±B)=tan⁡A±tan⁡B1∓tan⁡Atan⁡B\tan(A\pm B)=\frac{\tan A\pm\tan B}{1\mp\tan A\tan B}
sin⁡2A=2sin⁡Acos⁡A\sin 2A=2\sin A\cos A
tan⁡2A=2tan⁡A1−tan⁡2A\tan 2A=\frac{2\tan A}{1-\tan^2 A}
cos⁡2A=cos⁡2A−sin⁡2A\cos 2A=\cos^2 A-\sin^2 A
cos⁡2A=2cos⁡2A−1\cos 2A=2\cos^2 A-1
cos⁡2A=1−2sin⁡2A\cos 2A=1-2\sin^2 A

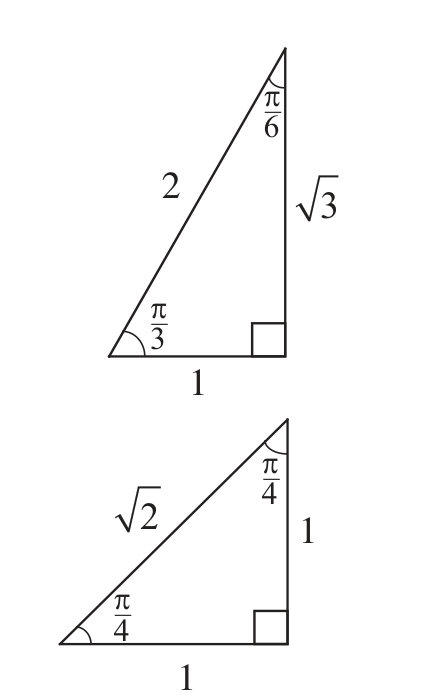
Products

2sin⁡Acos⁡B=sin⁡(A+B)+sin⁡(A−B)2\sin A\cos B=\sin(A+B)+\sin(A-B)
2cos⁡Asin⁡B=sin⁡(A+B)−sin⁡(A−B)2\cos A\sin B=\sin(A+B)-\sin(A-B)
2cos⁡Acos⁡B=cos⁡(A+B)+cos⁡(A−B)2\cos A\cos B=\cos(A+B)+\cos(A-B)
2sin⁡Asin⁡B=cos⁡(A−B)−cos⁡(A+B)2\sin A\sin B=\cos(A-B)-\cos(A+B)

Sums

sin⁡C+sin⁡D=2sin⁡(C+D2)cos⁡(C−D2)\sin C+\sin D=2\sin\left(\frac{C+D}{2}\right)\cos\left(\frac{C-D}{2}\right)
sin⁡C−sin⁡D=2cos⁡(C+D2)sin⁡(C−D2)\sin C-\sin D=2\cos\left(\frac{C+D}{2}\right)\sin\left(\frac{C-D}{2}\right)
cos⁡C+cos⁡D=2cos⁡(C+D2)cos⁡(C−D2)\cos C+\cos D=2\cos\left(\frac{C+D}{2}\right)\cos\left(\frac{C-D}{2}\right)
cos⁡C−cos⁡D=−2sin⁡(C+D2)sin⁡(C−D2)\cos C-\cos D=-2\sin\left(\frac{C+D}{2}\right)\sin\left(\frac{C-D}{2}\right)
Special angle triangles: 30-60-90 and 45-45-90

MEASUREMENT

Area=12absin⁡C\text{Area}=\frac{1}{2}ab\sin C
Area=12(a+b)h\text{Area}=\frac{1}{2}(a+b)h
Area=12r2θ\text{Area}=\frac{1}{2}r^2\theta
Arc length=rθ\text{Arc length}=r\theta
Volume=πr2h\text{Volume}=\pi r^2 h
Curved surface area=2πrh\text{Curved surface area}=2\pi r h
Volume=13πr2h\text{Volume}=\frac{1}{3}\pi r^2 h
Curved surface area=πrl\text{Curved surface area}=\pi r l
(where l = slant height)
Volume=43πr3\text{Volume}=\frac{4}{3}\pi r^3
Surface area=4πr2\text{Surface area}=4\pi r^2

Source: NZQA Level 3 Mathematics Formulae Sheet (91577-frm-2024)